1. 개요
- 인공신경망(Artificial Neural Network)에서 뉴런의 출력값을 결정하는 비선형 함수 의미
- 입력 신호의 가중합을 받아, 출력값을 비선형적으로 변환함으로써 복잡한 문제 해결 가능하게 하는 핵심 구성요소
- 선형 함수를 사용할 경우 신경망이 다층 구조를 갖더라도 단일층으로 환원될 수 있으므로, 모델 표현력 제한됨
- 활성화 함수는 입력과 출력 사이의 비선형성 도입을 통해 고차원 표현 학습 가능하게 함
- 일반적으로 각 뉴런에 독립적으로 적용되며, 주어진 입력값에 따라 출력값이 제한되거나 강조되는 효과 가짐
2. 활성화 함수의 필요성
- 비선형성 도입: 선형 회귀처럼 단순한 모델로는 XOR 문제 등 비선형 패턴 학습 불가능함
- 표현력 확장: 은닉층에서 다양한 특징 추출 가능, 모델의 학습 대상 범위 확장됨
- 계층적 학습 가능: 다층 신경망 구조가 계층별 의미 있는 표현을 학습하도록 함
- 경사하강법 기반 학습 가능: 미분 가능한 함수 사용 시 역전파(Backpropagation)를 통해 가중치 학습 가능
3. 주요 활성화 함수 종류 및 특징
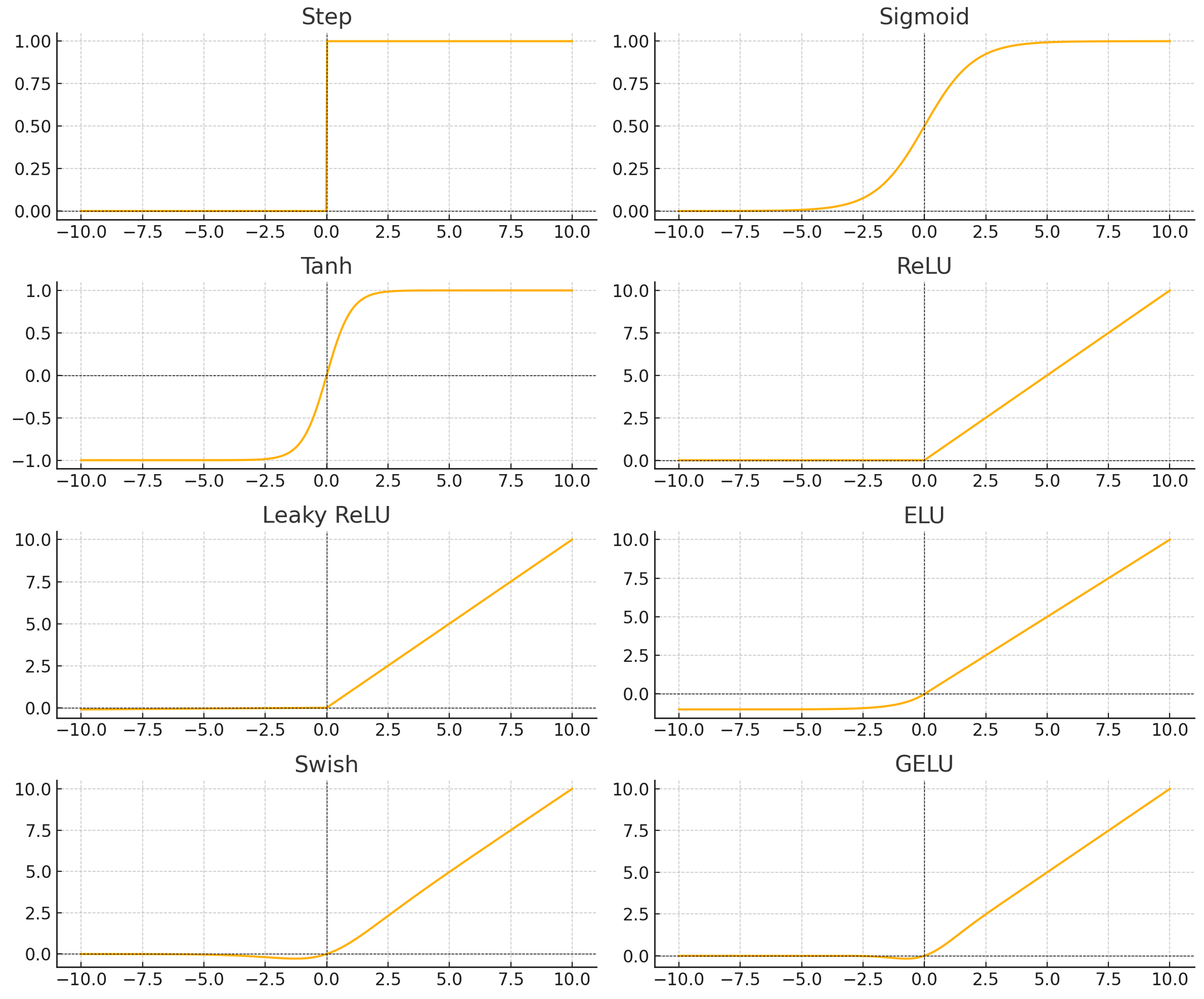
3.1. Step Function (계단 함수)
- 특정 임계값을 기준으로 0 또는 1 출력
- 수학적으로 간단하지만, 비미분성 문제로 역전파 불가능
- 고전적인 퍼셉트론 모델에서 사용
3.2. Sigmoid Function (시그모이드 함수)
- 수식: σ(x) = 1 / (1 + e^(-x))
- 출력 범위 (0, 1), 확률 해석 가능
- 기울기 소실(Vanishing Gradient) 문제 존재 → 큰 입력값에서 gradient가 0에 수렴
- 출력이 중심에 치우치지 않아 학습 속도 저하 초래
3.3. Tanh Function (쌍곡 탄젠트 함수)
- 수식: tanh(x) = (e^x - e^(-x)) / (e^x + e^(-x))
- 출력 범위 (-1, 1), 중심성이 있음 → Sigmoid보다 학습 효율 높음
- 그러나 여전히 기울기 소실 문제 존재
3.4. ReLU (Rectified Linear Unit)
- 수식: f(x) = max(0, x)
- 간단한 수식으로 계산량 적고, gradient 소실 문제 완화
- 음수 입력에 대해 gradient가 0이 되어 뉴런이 죽는 현상(Dead Neuron) 발생 가능
- 학습이 빠르고, 깊은 신경망에서 자주 사용됨
3.5. Leaky ReLU
- ReLU의 변형 형태로 음수 입력에도 작은 기울기 존재
- 수식: f(x) = x if x>0 else αx (0<α<<1)
- Dead Neuron 문제 완화 가능
3.6. Parametric ReLU (PReLU)
- Leaky ReLU의 α 값을 학습하도록 개선
- 모델이 데이터 특성에 맞게 α 자동 조절 가능
3.7. ELU (Exponential Linear Unit)
- 수식: x if x > 0, else α(exp(x) - 1)
- 입력이 음수일 때도 출력이 존재하여 중심성이 존재
- 출력 평균이 0에 가까워 학습 속도 향상 효과 있음
3.8. Swish
- 수식: f(x) = x * sigmoid(x)
- Google에서 제안한 활성화 함수로, ReLU보다 성능 우수함이 알려짐
- Smooth하고 미분 가능, gradient 흐름에 긍정적 영향
3.9. GELU (Gaussian Error Linear Unit)
- Transformer 계열 모델(BERT 등)에서 자주 사용됨
- 수식적으로 복잡하나 자연스러운 비선형성 제공
- 확률 기반 활성화 함수로 성능 면에서 우수하다는 연구 결과 존재
4. 선택 기준 및 비교
| 구분 | 출력 범위 | 비선형성 | Gradient 문제 | 계산량 | 사용 예 |
|---|---|---|---|---|---|
| Sigmoid | (0, 1) | 존재 | Vanishing | 낮음 | 이진 분류 출력층 |
| Tanh | (-1, 1) | 존재 | Vanishing | 낮음 | RNN 내부 |
| ReLU | [0, ∞) | 존재 | Dead Neuron | 매우 낮음 | CNN, DNN |
| Leaky ReLU | (-∞, ∞) | 존재 | 완화 | 낮음 | 일반 CNN |
| ELU | (-α, ∞) | 존재 | 완화 | 중간 | 깊은 네트워크 |
| Swish | (-∞, ∞) | 존재 | 없음 | 중간 | 최근 DNN |
| GELU | (-∞, ∞) | 존재 | 없음 | 다소 높음 | NLP (BERT 등) |
5. 실제 적용 사례
- CNN 기반 이미지 분류기: 대부분 ReLU 사용, 효율성과 학습 속도 때문
- NLP 모델: Transformer 기반 모델(BERT, GPT 등)에서 GELU 사용
- RNN 및 LSTM: Tanh와 Sigmoid 혼용하여 시계열 정보 유지
- GAN: Generator에서 Leaky ReLU, Discriminator에서 Sigmoid 사용되는 경우 많음
6. 최근 동향 및 연구
- Swish, Mish, GELU 등 학습 효율이 높은 새로운 활성화 함수 지속 제안 중
- 모델 구조뿐 아니라 활성화 함수 선택이 전체 모델 성능에 큰 영향 미침
- 자동 활성화 함수 선택(AutoML 관점), 함수 자체를 학습하는 Neural Architecture Search 등 연구 중
- ReLU의 단순성과 계산 효율로 인해 여전히 가장 널리 사용되는 함수로 자리 잡고 있음
7. 결론
- 활성화 함수는 신경망의 비선형성을 도입하여 복잡한 문제 해결을 가능하게 만드는 필수 구성요소
- 다양한 함수들이 존재하며, 각 함수는 적용 환경과 문제에 따라 선택 필요
- 모델 구조뿐만 아니라 활성화 함수의 선택 또한 전체 성능 최적화의 중요한 요소로 작용함
'IT Study > 인공지능 관련' 카테고리의 다른 글
| 🤖 생성형 AI(Generative AI) (0) | 2025.03.28 |
|---|---|
| 🤖 파인튜닝(Fine-tuning) (0) | 2025.03.28 |
| 🤖 자기지도학습(Self-supervised Learning) (0) | 2025.03.28 |
| 🤖 MLOps(Machine Learning Operations) (0) | 2025.03.27 |
| 💽 AI 기술을 위한 연산 처리 장치(CPU, GPU, NPU) (1) | 2025.03.27 |